An affine transformation is one that keeps lines parallel, but not necessarily angles and distances.
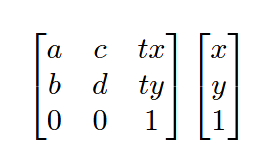
[ a c tx
b d ty
0 0 1 ]
a, b, c, and d are used for things like scaling, rotation, shear, and so on. tx and ty are translations. To use this, you will place your matrix with the x y coordinates on the right.
The identity matrix is
1 0 tx
0 1 ty
0 0 1
to rotate clockwise, when y axis is pointing down:
cos T -sin T tx
sin T cos T ty
0 0 1
How this would look in LaTeX
\documentclass{article}
\usepackage{amsmath} % Include the amsmath package
\begin{document}
\[
\begin{bmatrix}
a & c & tx \\
b & d & ty \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
1 \\
\end{bmatrix}
\]
\end{document}